Das Rentenkonzept

4.1.3.1 Konsumentenrente

Produzentenrente

Stellen Sie sich einmal vor, jemand spricht Sie auf der Straße unvermittelt an, er verkaufe Ihnen einen 100-Euro-Schein für 80 Euro. Sie begutachten den Schein und sind sich sicher, dass er echt ist. Kein doppelter Boden, kein Trick - alles ist bestens. Natürlich schließen Sie dieses gute Geschäft ab. Wann gibt es schon mal 100-Euro-Scheine für nur 80 Euro? Ein wahres Schnäppchen!

Das wird natürlich nicht passieren. Und wenn doch, dann würden Sie Zweifel beschleichen, ob denn alles seine Richtigkeit hätte. Vielleicht würden das Geschäft aus Angst, übervorteilt zu werden, doch nicht abschließen. Ein ganz ähnliches Geschäft schließt der Autor aber in seinen Lehrveranstaltungen mit seinen Studenten ab - allerdings mit deutlich geringeren Beträgen, denn er will ja nicht arm dabei werden. Er verkauft - in begrenzter Anzahl, versteht sich - Ein-Euro-Stücke für 60 Cent. Die Studierenden erkennen sofort, dass die Münzen echt sind. Es besteht keinerlei Gefahr, übervorteilt zu werden.

Wozu dieses anscheinend unsinnige Geschäft? Nun, der Autor kennt ie Zahlungsbereitschaft seiner Studenten für Ein-Euro-Münzen im Unterschied zu vielen anderen Gütern im Voraus. Sie beträgt 99 Cent. Zu diesem Preis würde er säckeweise Ein-Euro-Münzen an den Mann bringen. Er könnte bei größeren Mengen vermutlich sogar 99,5 Cent, wenn nicht noch mehr verlangen. Bei anderen Gütern - wie z. B. einem Müsli-Riegel oder einer Schachtel Büroklammern - könnte er die Zahlungsbereitschaft der Studierenden offensichtlich nicht so gut abschätzen - wenngleich er eine Methode kennt, mit der er sie ziemlich genau ermitteln könnte.

Wenn er nun einen Studierenden fragt, der ein Ein-Euro-Stück für 60 Cent erworben hat, er möge angeben, was ihm dieses Geschäft "gebracht habe", dann ist die mit an Sicherheit grenzender Wahrscheinlichkeit zu erwartende Antwort: "40 Cent." Bisher hat es jedenfalls immer geklappt. Diese 40 Cent sind die Konsumentenrente aus dem abgeschlossenen Geschäft.

Da die Konsumentenrente in Geldeinheiten gemessen wird, lässt sie sich über Personen aggregieren. Die gesamte Konsumentenrente, die die Studierenden aus den 1-Euro-Verkäufen des Autors realisieren, ist einfach die Summe der individuellen Renten.

Die Konsumentenrente lässt sich im Marktdiagramm abbilden. Dazu betrachten wir noch einmal das Beispiel, mit dessen Hilfe wir im Rahmen der kardinalen Nutzentheorie die Nachfrage eines Individuum nach Bier abgeleitet hatten. Die gewonnene Nachfragefunktion lautete

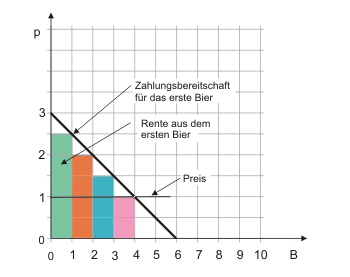
mit $B$ als Zahl der Biere und $p$ als Preis je Glas. Diese (individuelle) Nachfragefunktion ist in Abbildung 1 wiedergegeben. Es sei noch einmal darauf hingewiesen, dass in der Nachfragefunktion zum Ausdruck kommt, was der Konsument für jeweils eine weitere Einheit des Gutes zu zahlen bereit ist. Diese Zahlungsbereitschaft entspricht seinem Grenznutzen. Die Nachfragefunktion ist ja auch nichts anderes als die Abbildung der Grenznutzenfunktion des Konsumenten.

Abbildung 1

     

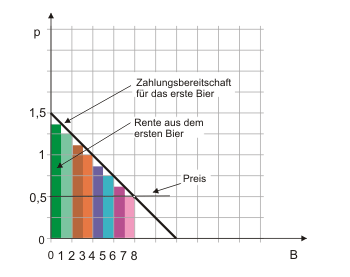
Abbildung 1 lässt erkennen, dass die Zahlungsbereitschaft des Konsumenten für das erste Bier 2,50 Geldeinheiten beträgt, für das zweite Bier 2,00, für das dritte 1,50 und für das vierte 1,00. Beträgt der Preis 1,00 Geldeinheit, wird der Konsument vier Bier kaufen. Aus dem ersten Bier hat er eine Rente von 1,50, aus dem zweiten von 1,00, aus dem dritten von 0,50 und aus dem vierten von 0,00 - zusammen also eine Konsumentenrente von 3,00 Geldeinheiten. Dies entspricht offensichtlich der farblich markierten Fläche unter der Nachfragefunktion und oberhalb des Preises.

Wir hätten die Konsumentenrente auch wie folgt berechnen können: Die Zahlungsbereitschaft für 4 Bier beträgt 7,00 Geldeinheiten (farbige Flächen). Die Ausgaben für vier Bier betragen 4 Geldeinheiten. Die Differenz zwischen Zahlungsbereitschaft und Ausgaben ist die Konsumentenrente aus dem Bierkonsum.

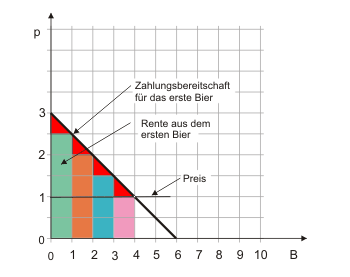
Die Zahlungsbereitschaft des Konsumenten wird durch die Fläche unter der Nachfragefunktion angegeben. In Abbildung 1 sind unter der Nachfragefunktion aber noch kleine weiße Dreiecke zu erkennen, die wir bei der Berechnung der Zahlungsbereitschaft von von 7 Geldeinheiten nicht berücksichtigt haben. Sie werden in der maussensitiven Abbildung rot eingefärbt, wenn Sie das Bild anklicken.

Abbildung 2

Diese weißen Dreiecke verschwinden, wenn wir den Konsum des Bieres in beliebig kleinen Einheiten zulassen. Um dies zu verdeutlichen sind in Abb. 2 die bisherigen Biere nur noch halb so groß. Gleichzeitig halbiert sich natürlich auch der Preis. Anstelle von 4 "ganzen" Bieren würde unser Konsument nun 8 "halbe" Biere kaufen wollen. Es ist deutlich zu erkennen, dass die Fläche der weißen Dreiecke nun nur noch halb so groß ist wie in Abbildung 1. Je kleiner die Einheiten werden, desto kleiner werden auch die weißen Dreiecke. Schließlich verschwinden sie bei unendlicher Teilbarkeit der Produkte vollkommen:

Etwas formaler kann das wie folgt erklärt werden: Die Nachfragefunktion ist die Grenznutzenfunktion, also die erste Ableitung der Nutzenfunktion. Die Fläche unter der Grenznutzenfunktion ist das unbestimmte Integral der Nutzenfunktion. Da wir den Nutzen von null Bieren auf null normiert haben, gewinnen wir durch Integrieren der Nachfragefunktion (1) die Höhe des Nutzens (umgekehrt liefert die Ableitung von (2) die Nachfragefunktion (1)):

Der Nutzen von 4 Bier ist $U = 8$. Damit ergibt sich als maximale Zahlungsbereitschaft für 4 Bier ein Betrag von 8 Geldeinheiten. Bringen wir davon die Ausgaben in Höhe von 4 in Abzug, verbleibt eine Komsumentenrente von 4, die wir in Abbildung 3 als dreieckige Fläche unterhalb der Nachfragefunktion und oberhalb des Preises erkennen können.

Abbildung 3

Abbildung 4

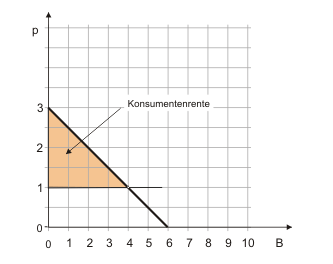
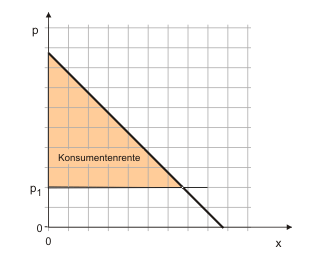
Abbildung 4 betrachtet nun nicht mehr das einzelne Individuum im Zahlenbeispiel, sondern den Markt. Da die Marktnachfrage nichts anderes darstellt als die aggregierten individuellen Nachfragefunktionen, entspricht die Fläche unter der Marktnachfragefunktion und oberhalb des Preises der aggregierten Rente aller Nachfrager, die hier zum Preis p₁ das Produkt x erwerben. Ebenso hätte man selbstverständlich alle individuellen Renten aufaddieren können. Das ist ohne Weiteres möglich, da die Renten ja in Geldeinheiten gemessen werden. Wir halten damit als wichtiges Ergebnis fest:

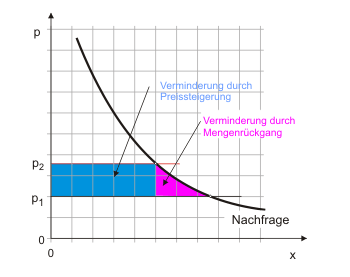
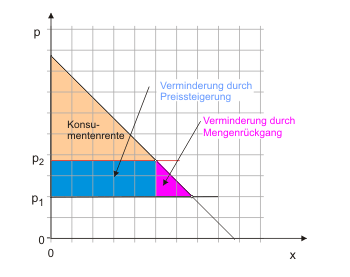
Die Konsumentenrente ist ein Maß für das Wohlergehen (die Wohlfahrt) der Nachfrager. Sie misst den Nutzenüberschuss ("surplus") über die Ausgaben. Den Konsumenten geht es natürlich um so besser, je geringer der Gleichgewichtspreis ist. Umgekehrt verlieren sie Rente, wenn der Preis steigt. Diese Situation zeigt Abbildung 5. Man erkennt zwei Gründe, die für den Rückgang der Konsumentenrente verantwortlich sind. Erstens führt der steigende Preis zu verminderter Nachfrage. Aus den Gütereinheiten, die die Konsumenten nun nicht mehr erwerben, kann natürlich auch keine Rente mehr resultieren. Zweitens vermindert der gestiegene Preis die Rente aus jedem noch stattfindenden Kauf genau um die Preisdifferenz $p_2 - p_1$.

Abbildung 5

Wie wohl jedes einfache Konzept ist auch das der Konsumentenrente nicht frei von Kritik. Der schärfste Kritikpunkt setzt an der Herleitung mit Hilfe der kardinalen Nutzentheorie an, denn die Fläche unter der Nachfragefunktion wird als in Geldeinheiten bewerteter Grenznutzen der Konsumenten aufgefasst. Dies ist jedoch nicht ganz so kritisch, wie es zunächst scheinen mag. Nachfragefunktionen lassen sich über das Indifferenzkurvenkonzept herleiten, das ohne die kardinale Nutzenmessung auskommt. Und entscheidend ist dann nur, dass man an der Nachfragekurve die Zahlungsbereitschaft der Konsumenten ablesen kann. Das ist aber unstrittig. Wenn man die Marktnachfrage empirisch ermitteln kann, dann kann man sie ohne Weiteres als Kurve der maximalen Zahlungsbereitschaft der Konsumenten für alternative Mengen des Gutes interpretieren.

Damit sind wir aber auch schon beim zweiten Kritikpunkt. Selbst wenn man die Nachfragefunktion ermitteln könnte (denken Sie an das Identifikationsproblem, dann würde es einem doch immer nur für den Bereich gelingen, für den man auch Beobachtungen hätte. Zur Berechnung der Konsumentenrente wird jedoch die gesamte Nachfragefunktion benötigt. Und wie will man wissen, wie die Nachfragefunktion in extremen Bereichen Bereichen verläuft, bei sehr hohen oder extrem niedrigen Preisen, die man bisher noch nicht beobachten konnte (dieses Problem haben wir im Zusammenhang mit Angebotsfunktionen schon einmal betrachtet)? Niemand kann sagen, welche Menge Benzin zum Preis von 50 EUR oder zum Preis von 10 Cent je Liter getankt würde.

Abbildung 6

     

Doch glücklicherweise ist auch die in Teilbereichen unbekannte Marktnachfrage kein wirkliches Hindernis, wenn man Überlegungen mit Hilfe der Konsumentenrente anstellen möchte. Was nämlich in der Regel interessiert, sind Veränderungen der Konsumentenrente, die z. B. durch eine Steuererhöhung, einen Höchstpreis oder andere staatliche Eingriffe wirtschaftspolitische Eingriffe in einen Markt ausgelöst werden. Um diese Änderungen berechnen zu können, muss man die Höhe der Rente selbst gar nicht kennen - ebenso wie man für eine Veränderung des Wasserstandes nicht notwendig zuerst messen muss, wie tief ein See ist. Es genügt eine kleine Messlatte am Ufer.

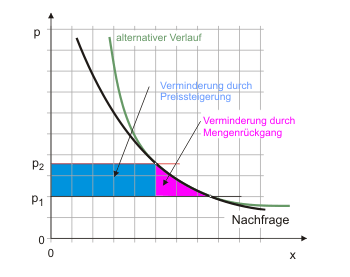
Wie man aus Abbildung 6 unmittelbar erkennen kann, reicht es, die Marktnachfrage im relevanten Teilbereich zu kennen, um die Auswirkungen einer Preisänderung auf die Konsumentenrente berechnen zu können. Wenn Sie Abbildung 6 anklicken, werden Sie sehen, dass der Verlauf der Nachfragefunktion außerhalb des betrachteten Bereichs für die Berechnung der Veränderung der Konsumentenrente keine Rolle spielt. Das gilt natürlich nicht mehr, wenn der Preis noch über p₂ hinaus anstiege.

|           | Impressum